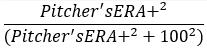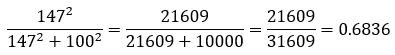Hello again, my HHS friends! Dr. Doom here again. Thanks for bearing with me through those first two parts; I know they were review for most of us, but I figured I should make sure to explain everything, just in case someone new needed a primer. In any case, welcome to the final part of the series. As always, a special thanks to Doug for posting these, and to the community for tolerating them. This truly is a great place to talk baseball on the web.

As you’ll recall, in Part 1 we discussed the Pythagorean Record and how innings pitched relate to decisions. In Part 2, we saw how ERA+ works. Now, using those tools at our disposal, it’s time to build our WAR paradigm! More after the jump.

Let’s start with getting a record for a pitcher based on ERA+. I’m going to pick on Dizzy Dean in 1937, because… why not? This is always what Bill James does in his writing – just picks a random player in a random year to make a point about something unrelated. So I figure I’m in good company. Regardless, in 1937, Dizzy Dean had his last halfway-decent season. He went 13-10 with a 2.69 ERA. He was no longer leading the league in strikeouts, but he still posted the best walk rate in the league.

Anyway, germane to our discussion, he posted a 147 ERA+ in 197.1 innings. The first thing we need to ask ourselves is, “How many decisions did he deserve?” To discover the answer, we simply divide innings pitched by nine. 197 1/3 divided by 9 is 21.93, which we’ll call 22. He actually got 23 decisions, so we’re starting by removing one of those. Hopefully, you’re with me so far.

Now, the next step is the “math” step. If you’re squeamish about math, I will try not to lose you, but it’s pretty simple arithmetic. What you’re going to do here is figure out the Pythagorean Winning % based on the pitcher’s ERA+. Now, when I introduced the Pythagorean Record, I pointed out that it’s figured by putting runs scored in the numerator and both runs scored and runs allowed in the denominator. Of course, what we don’t have today is runs scored. So what we’re going to do is assume an average offense. We do this with the number 100. Pythagorean records hold with ratios. In other words, plugging in 800 runs scored and 600 runs allowed will give you the same Pythagorean Record as 4 runs scored and 3 allowed. So what we do here is use 100 as an average offense (since a 100 ERA+ would be an average pitcher).

Normally, what this would look like is this: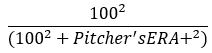

That might seem right to you… but it’s WRONG. You see, this is where we get into the problem of reciprocals. ERA+ is “inverted,” as you may remember, meaning that the “wrong” thing is in the numerator and the wrong thing in the denominator. If you use ERA- or FIP-, the above formula is correct. If you use ERA+, you have to turn it around. It looks, correctly, like this:

In the case of Dizzy Dean in 1937, we have:

Now that we know his “winning percentage”, we can apply it to his number of decisions – which, you’ll recall, was 22. That gives us 15.04 wins (we can safely round down, I think), for a 15-7 record. Dizzy Dean was actually 13-10 in 1937, but deserved to be 15-7. Dizzy Dean was 2.5 games better than his record indicates in 1937.

So, to recap, we’ve used wins, winning percentage and ERA+ to arrive at the number of wins we think a pitcher deserved (as an aside, Bill James, in his Hall of Fame book titled, in different versions, Whatever Happened to the Hall of Fame or The Politics of Glory, introduced a cute little method to bring wins and winning percentage into a single unit: it’s simply wins * winning% + wins – losses. It’s a cute little formula, and works decently for putting a whole career on a one-number scale. Play around with it, if you like.) 

But, how does this get us to WAR? Well, this is the fun part. First, you pick a replacement level. Let’s say you think “replacement” is nonsense, and it’s all about average. Fine. That’s easy. In Dizzy Dean’s 22 appearances, an average pitcher would’ve gone (duh) 11-11. Dizzy “went” 15-7. That means he’s 4 wins above average, as he won four games that an average pitcher would’ve lost.

But let’s say you think it’s more complicated than that. Let’s say you think a replacement pitcher would’ve had a .375 winning percentage – this is what the Baseball Gauge uses for its “bench” feature – 75% of average. Fine. That works out to a replacement pitcher winning 8.25 games out of 22. Dizzy won 15, which makes him 6.75 Wins Above Replacement. If you like the .294 winning percentage used by Baseball-Reference and FanGraphs, you get 6.5 replacement level wins, which gives 1937 Dizzy 8.5 WAR (rather than the 4.5 and 4.8 WAR that B-R and FanGraphs actually credit him with).

So… why look at WAR this way? Well, it’s easy to calculate, it’s a FUN way to play with sabermetrics, and it lets us compare starters to relievers. For example. In part two, I told you about Rollie Fingers‘ 333 ERA+ in the 1981 strike year. That’s great, obviously. But what does it mean? How do I compare it to Dizzy Dean in 1937, for example? Well, Diz was 4 games better than “average,” right? I have Rollie in 1981 deserving 8.66 decisions, which we’ll call 9, giving him the benefit of the doubt. This method has him deserving an 8-1 record. That’s 3.5 wins above average, which allows me to definitively say that, relative to average, Dizzy Dean’s 1937 was a better season than Rollie Fingers’ 1981 – in spite of Fingers’ season having more than double the ERA+.

As shown above, this method lets us figure out how many wins we think a pitcher really deserved. Was Walter Johnson hosed by playing with the Senators? Sure he was. How much, though? Well, his historical record will tell you that he went 417-279. By this method, I have him deserving of a 449-207 record for a .684 winning percentage, instead of the .599 he actually posted (applying that .684 to Johnson’s 696 actual decisions yields 476 wins, 59 more than his actual total). Bottom line is Johnson was SUPER cheated toiling for the Sens, and we can put a number on it. If we use a .300 winning percentage as “replacement,” a replacement-level pitcher would’ve gone 197-460. That means Johnson deserved to win 252 more games than a replacement player! 

Some other notables look like this: Cy Young is at 291 wins above replacement level; Sandy Koufax at 86; Bob Gibson at 137; Randy Johnson at 160; Kevin Brown at 115 (note that Kevin Brown is well ahead of Sandy Koufax; I think I’ve made my position on that matter clear in COG voting, but just wanted to reiterate). In case you’re wondering about our test case: while Dizzy Dean’s 1937 record is improved by this method, he actually loses his 30-win season and moves down to a total of 138 wins, rather than the Gashouse-Gang-inflated 150 that he actually won.

I like to think this is a fun little tool for comparing pitchers, for a “20-win season” to still mean something (no one can manage a 20-WAR season as standard WAR is calculated), and I think it’s fun to develop little tools (much as Bill James does, the master at this sort of thing). It’s fun to remember that ANYONE can do this kind of thing, if we just give it some time and thought.

Well, I hope you all enjoyed this little tool. Feel free to play around with it. Find something interesting? Pass it on! Think it’s cool that Mariano deserves a 115-27 record (not 82-60)? I think so, too! (And it’s darn close to Dizzy Dean’s numbers, considering Mariano was just a ninth-inning guy basically his whole career, while Dean is in the Hall of Fame as a starter). Did those few years as a reliever cost John Smoltz the chance at 300 wins? No; but you’re welcome to try to make the numbers work out, if you’d like. Would Catfish Hunter be in the Hall if he had a 199-184 record, like he actually deserved?  I doubt it. How would we feel about Pedro‘s 2000 season had he gone 22-2 (!!!!!), like he should’ve? I don’t know, but that would’ve been awesome. Should Bob Gibson have won 30 in 1968? I’ll let you figure it out, in case you want a little homework. I’d love to hear if you have any thoughts on this. I look forward to your comments, and thank you for tolerating my ramblings in this series!

For those who would like to try out the new metric, a spreadsheet with a pivot table has been prepared for expansion era pitchers, and includes every 50+ IP season since 1961. There you can select individual pitchers and compare FanGraphs WAR (fWAR) with the new WAR metric (nWAR) based on FanGraphs ERA+ measure (it’s actually 10,000 divided by FanGraphs ERA- metric). To use the Pivot table:

1. Download the spreadsheet from the link above, and open in Excel. 
2. In the top left of the Pivot table, click on the filter symbol (hourglass) beside the pitcher’s name and search for the pitcher you want to see by typing his name (first and last) in the Search box and click on his name when it appears in the search results.
3. Wait a second or two, and the individual season results will be displayed in the table.

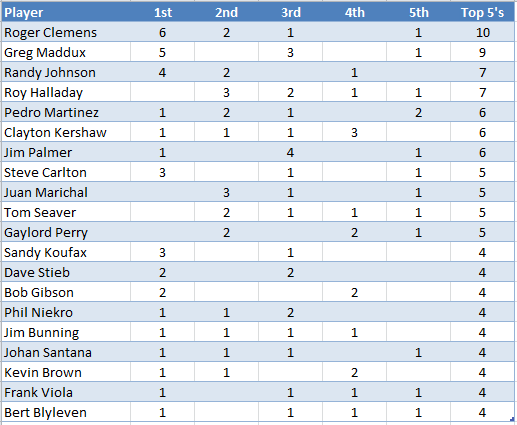
Also in the spreadsheet is a list of the Top 5 nWAR results for each season since 1961. The tale of that tape looks like this: