Greetings, HHSers from Dr. Doom!
OK, so here’s the thing. This website is called “High Heat STATS.” And while Doug will occasionally enlighten us with a beautiful, table-filled column about some statistic or other through time, I think we all just like talking baseball. But in this series of posts, I’m going to get into the nitty-gritty of building a mock-WAR that I think you’ll all enjoy. It’s a quick-and-dirty way to do a couple of things I think are important.
- It takes ERA (or FIP) numbers and prioritizes them over won-lost records;
- It allows (more) direct comparisons of starters and relievers;
- It simplifies down to one dimension VERY quickly and easily (or stays two-dimensional, if you prefer);
- It is easily figured with a computer/calculator and only TWO stats, easily found on Baseball-Reference or Fangraphs.
I haven’t been posting much lately, and I apologize for that. My wife and I moved and had to maintain two residences for a couple months, and I just helped my parents move. I’ve been settling in at a new job, and I also don’t really have my own PC anymore. So the chances to comment have been limited. That said, I have kept up reading every post, and most of the comments. But for the time being, I thought I’d jump back in to writing a few posts of my own. As always, a special thanks to Doug for posting this for me.
In this first part of the series, most of you are probably going to be bored, but I’m going to post this anyway so that those who don’t know can learn. We’ll start by talking about a Pythagorean Record. First of all, the Pythagorean Record was invented by Bill James, not Pythagoras. But it does use the squaring of two numbers to discover a third number, just as happens in the Pythagorean theorem, so there’s that.
The Pythagorean Record is a way of assessing how many games a team “deserved” to win, based on the number of runs they scored or allowed. It works by squaring the number of runs scored, and dividing that by the sum of the square of runs scored and the square of runs allowed, like this: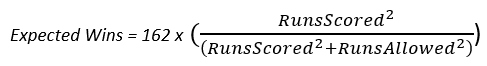
Let’s take a totally random example: last year’s Pittsburgh Pirates (by the way, I didn’t check how well this would work before picking the example, so I’m glad this one basically works out). The Pirates scored 668 runs. They allowed 731 runs. Therefore, we calculate their Expected Wins like this: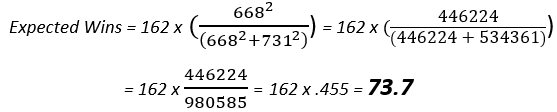
This says the Pirates should’ve won 45.5% of their 162 games, or 74 games (well, 73.7, but we have to use whole numbers, since that’s how wins work). In fact, they actually won 75. That’s ridiculously close for a simple estimate like this. (Note: I realize that there are actually more accurate ways than squaring to get this to work; an exponent of 1.82 is said to work better, and usually it does. There’s also a variable exponent you can use based on the run environment of the league in question, but all of that is, for this discussion, so much fussing about, because in its original incarnation, we get VERY good results AND beautiful simplicity with the simple exponent of 2, so that’s what I’ll just be using here.)
That’s Pythagorean Record. The other thing that we need to discuss is something that doesn’t have a name, as far as I know, but could be described as “decision proportion.” There is, and this will surprise no one, one pitching win credited for every (roughly) 9 innings pitched. This is probably not a surprise. Some of you might be expecting it to be a little more (“What about extra inning games?”), but keep in mind that MANY games end without a home team batting in the 9th, and some (though not many) games end even earlier because of weather.
Picking a league totally at random, the 2017 MLB had 43257 IP. Divide by nine and you get 4806 pitching decisions. There were 2430 games played last year; a win and a loss for each makes 4860 expected decisions. Decently close. We could adjust the numbers so we got an exact number of decisions, but we’re not actually looking to do that; take what I said above about beautiful simplicity and keep it in mind. I’m looking for ease and elegance here, not strict accuracy.
Let’s tray another one. In 1987, there were 37574.2 IP in 2105 games. We would expect 4175 decisions, we actually got 4210 (again, off by about 50 decisions). In 1954, there were 22126.2 IP, which leads us to expect 2459 decisions, instead of the 2462 we actually got (only off by 3). As you can see, it gets us within 2% of the total number of decisions, and often within 1%.
These two ideas, of the Pythagorean Record and “decision proportion”, are going to form the foundation of the WAR metric I’m going to introduce (and horse around with) in the third part of this series. But, before we get to that, in part 2 we’re going to talk about ERA+ and FIP.
Please feel free to comment away, though I’m sure there won’t be too much to say here, as these concepts are not too earth-shattering (especially if you’ve been in this community, or one like it, for a while). But, I hope you’ll all bear with me as things will get more interesting next time. Catch you in the next post!
